Termodinamik ( 1 )
Termodinamik bir bilim dalı olmakla birlikte dinamiğin alt dalı gibi düşünülür. Fakat termodinamik kendine özgü kanunları olan enerji, sıcaklık, iş ve ısı arasındaki ilişkiyi inceleyen temek bir bilim dalıdır.
Termodinamik kavramı Yunanca Modern Yunanca: thermos (ısı) ve Modern Yunanca: dynamic (enerji) kelimelerinden türetilmiştir. Bazı Türkçe kaynaklarda ısıl devingi olarak da geçer. Enerji, ısı, iş, entropi ve ekserji gibi fiziksel kavramlarla ilgilenir. Termodinamik yasalarının istatistiksel mekanikten türetilebileceği gösterilmiştir. (Kaynak: Wikipedia)
Termodinamik yazı dizimiz iki kısımdan oluşmaktadır. Şu anda 1. kısımda bulunmakta olup Termodinamik 2 için tıklayınız.
TERMODİNAMİK
Termodinamik Nedir? Termodinamiğin Tanımı
Enerji ve kuvvet uygulanmış cisimlerin incelenmesi anlamına gelen Termodinamik fiziğin ısı ile enerji arasındaki bağlantılarını inceleyen ve enerjinin şekil değiştirmesi ile uğraşan kolu olarak tanımlanır. Termodinamikte bir maddeye iş veya ısı verdiğimiz zaman maddenin hal değiştirmesi için, maddeye ne kadar iş veya ısı verilmesi veya alınması gerektiği hesaplanır. Termodinamikte diğer bir hedef de ısının ise çevrilmesi yöntemleri ve düşük sıcaklık kaynağından yüksek sıcaklık kaynağına ısı nakletmek için ne kadarlık bir iş verilmesi gerektiğini tespit etmektir.
Sanayinin 18. Yüzyılda büyük atılımlar yapması, geliştirilen makinaların çalıştırılabilmesi için insan ve hayvan gücünün yetersiz kalması, bazı bölgelerde akarsulardan faydalanma imkanlarının bulunmaması, buhar makinasının icadına yol açtı 1712 yılında ilk buhar makinasının yapılması, 1770 yılında James Watt tarafından bu alanda büyük gelişmeler sağlanması yakıtlardan daha ucuz, kolay ve verimli iş elde edilmesi araştırmaya yönelterek Termodinamik biliminin doğmasına sebep oldu. Buhar ve Gaz Türbinleri, Benzin Diesel Motorları, Soğutma Makinaları gibi tüm termik makinaların çalışma prensiplerinin araştırılması Termodinamiğin konularını kapsamaktadır.
Termodinamikte Kullanılan Kavramlar
Termodinamik işlemlere geçmeden önce bu bölümde sık kullanılan kavramları iyi öğrenmek gerekecektir.
Termodinamik Sistem
Kavramı belirli bir kütleyi veya uzayın incelenmek üzere ayrılan bir bölgesini belirtir. Şekil(5.1)
Çevre
Sistemin dışında kalan kütle veya bölgedir. Şekil(5.1)
Sınır
Sistemi çevresinden ayıran gerçek veya hayali yüzeydir. Sistemin sınırları hareketli veya sabit olabilir. Sınır, sistem ile çevresinin ortak temas ettiği yüzey olarakta tanımlanabilir. Matematiksel açıdan, sınırın kalınlığı sıfırdır, bu nedenle kütlesi ve hacmi yoktur. Şekil(5.1)
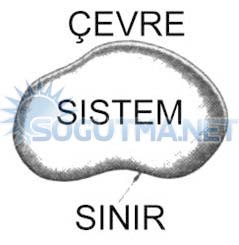
Sistem, çevre ve sınırın resim üzerinde gösterilmesi.
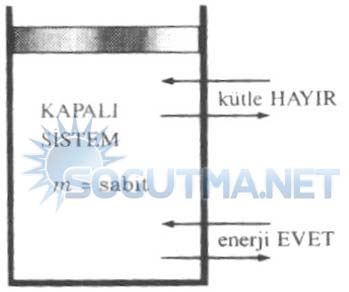
Kapalı Sistem (Kontrol kütlesi)
Sınırlarından kütle giriş çıkışı olmayan sabit bir kütledir.
Şekil 5.2
Kapalı sistem sınırlarından kütle geçişi olmaz, fakat enerji geçişi olalabilir.
Şekil 5.3
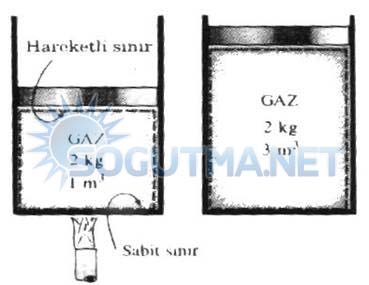
Hareketli sınıra sahip bir kapalı sistem.
Şekil 5.3’te gösterilen düzenekte 1nolu sisteme ısı akışı olduğunda belirli bir süre sonra 2 konumuna gelecektir. Sistemde kütle alış verişi olmadığı için kapalı bir sistemdir. Sisteme enerji transferi olduğundan sınırların bir bölümü hareket etmiştir.
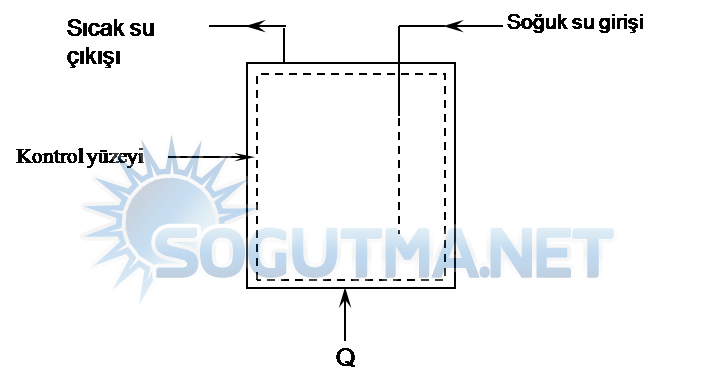
Açık sistem (Kontrol hacmi)
Termodinamik olarak incelenmek üzere göz önüne alınan belirli bir hacme denir. İçinden kütle ve enerji giriş çıkışı olan bir sistemdir.
Şekil 5.4
Bir girişli ve çıkışlı açık sistem (kontrol hacmi).
Şekil 5.4’teki termosifonda sürekli su giriş ve çıkışı olmaktadır. Q ısı kaynağından termosifondaki suya ne kadar ısı taşınımı olduğunu bulmak için sabit kütleyi seçmek doğru olmaz. Bunun yerine kontrol hacmine giren sıcak ve soğuk su akışlarını çıkan kütleler alarak suya taşınan ısı miktarını bulabiliriz.
Ayrık (İzole) Sistem
Sınırlarından enerji ve kütle geçişi olmayan sistemdir. Ayrık sistem üzerinden çevrenin hiçbir tesiri olmadığı kabul edilecektir.
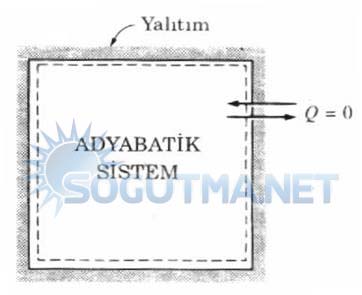
Adyabatik Sistem
Şekil 5.5
Adyabatik bir hal değişimi sırasında sistemle çevresi arsında ısı geçişi olmaz.
Tersinirlik Geri Dönüşebilirlik
Denge durumundaki bir sistem herhangi bir etkiyle hal değiştirdikten sonra hem sistemi hem de çevresini başlangıçtaki denge haline, getiriyorsa yapılan işlem tersinir bir işlemdir. (Şekil 5.6-a,b)

Şekil 5.6 a Şekil 5.6 b
Şekil 5.6 a.b
Tersinir bir işleme örnek
Şekil 5.6-a’daki F1 kuvvetinin şiddeti küçültür.
Şekil 5.6-b’deki konuma dönecek çevreyle ısı verişi ve sürtünme kuvveti olmadığı kabulüne göre F2 kuvveti F2−F1 kadar artırılırsa yani F bir olursa sistem tekrar eski haline gelecektir.
Tersinmez İşlem
Çevre sistem üzerine bir miktar net iş yapar ve bu nedenle ilk haline dönmez. (Şekil 5.7)

Şekil 5.7
Tersinmez bir işleme örnek
Şekil 5.7‘de sistem sıcaklığı T1, çevre sıcaklığı T2’ye ulaşıncaya kadar Q ısısını alacaktır. Herhangi bir işlem uygulanmadan bitiş durumundaki sistem kendi kendiliğinden başlangıçtaki haline dönemeyecektir.
Termodinamik İşlemler
Isı transferi ile ilgili tüm işlemlerde en az kayıpla sistem tasarımı hedeflenir. Soğutma işleminin sağlanmasında da gene en az enerji tüketimiyle belirli bir soğutma yükünün karşılanması istenir. Soğutma çevrimin meydana getiren her bir işlemin en az kayıpla ve en az enerji sarfıyla çalışması gerekir. Soğutma çevrimlerinde kullanılan bazı termodinamik işlemler aşağıda açıklanmıştır.
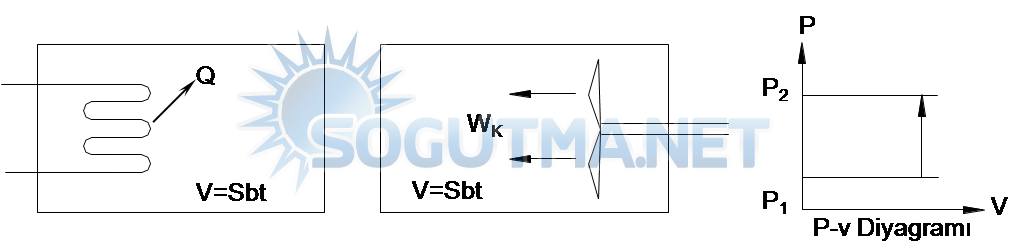
Sabit Hacimde Termodinamik İşlem (İzometrik)
Şekil 5.8 a’da elektrikli rezistanstan kapalı hacimde bulunan gaz akışkana Q ısısı verilmiş,. Şekil 5.8 b’de Wk işi verilmiş kapalı bir sistem olduğu için diyagramında 5.1’de görüldüğü gibi basıncın P1’den P2’ye çıkmasına neden olmuştur.
Şekil 5.8
Sisteme verilen ısının ve işin kapalı bir sistemde basınç hacim ilişkisi
Sabit Basınçta (İzobar)
Şekil 5.9’da sisteme verilen Q ısısı, piston sürtünmesiz, piston kütlesi ve atmosfer basıncı değişmediği kabulüne göre piston 2 konumu olarak sistemin basıncı sabit kalacaktır. Diyagram 5.2’de görüldüğü gibi.
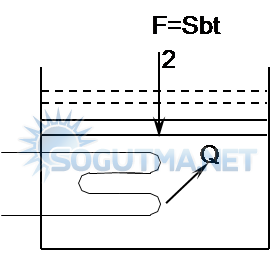
Şekil 5.9
Sabit hacimin deney düzeneğinde gösterilmesi
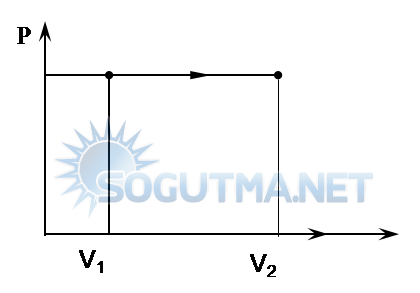
Diyagram 5.2
Sabit basınçta P−V diyagramı
Sabit Sıcaklıkta (İzotermik)
Aşağıdaki P.V diyagramında P1 basıncında 1-2 arası sabit basınçta olup sistem q1,2 ısısını alarak sabit sıcaklık ve basınç altında, P3 basıncında ise 3-4 arası sabit basınç altında olup sistem 3 noktasından itibaren q3,4 ısısını atmosfere transfer ederek 3 noktasından itibaren sabit sıcaklık ve basınç altında 4 noktasına kadar sıkıştırılmaktadır.
P1 basıncında 1-2 arasında sabit sıcaklık ve basınç altındaki genişleme q1,2 ısısını alarak gazın halini değiştirmekte,P3 basıncında 3-4 arasındaki sabit sıcaklık ve basınç altındaki sıkıştırma q3-4 ısısını atmosfere transfer edip 4 noktasındaki. gazın halini değiştirmektedir. Soğutma çevrimlerinde olduğu gibi.
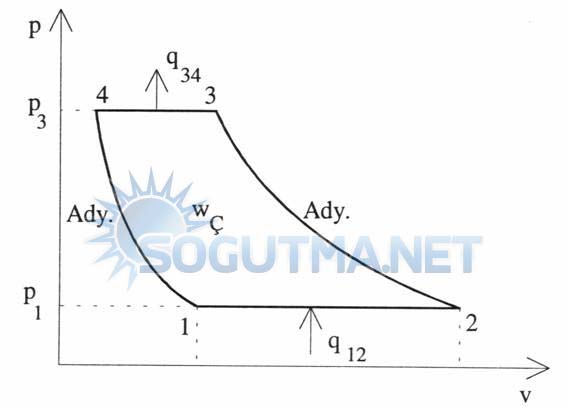
Diyagram 5.3
Sabit sıcaklıkta P-V diyagramı.
Sabit Entropi (İzentropik) Veya Geri Dönüşebilir Adyabatik
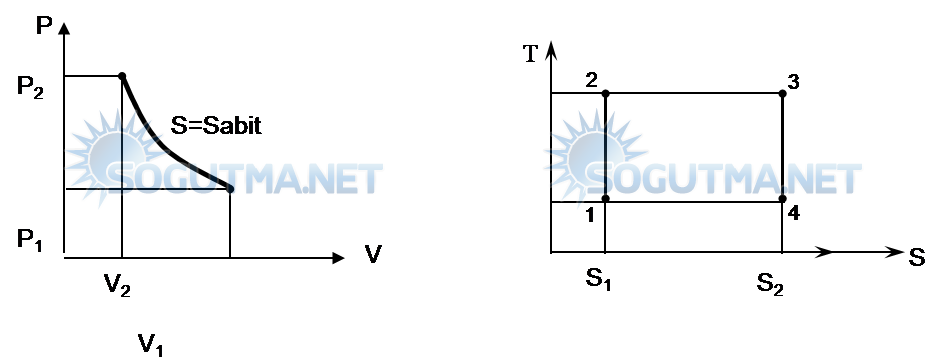
Diyagram 5.4
İzentropik işlemin P-V ve T-S diyagramında gösterilmesi
Termodinamik Kanunları
Termodinamik kanunlarını ayrıntılı olarak Termodinamik Kanunları yazımızda ele almıştık. Bu nedenle burada kısa özet şeklinde geçiyoruz. Merak edenler Termodinamik ve Termodinamiğin Yasaları yazımızı inceleyebilirsiniz.
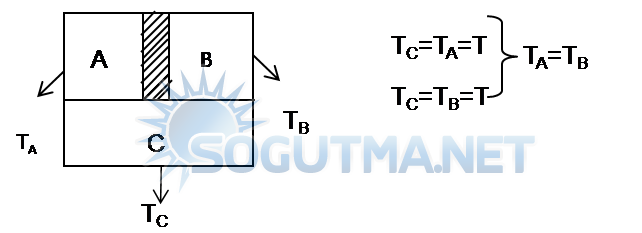
Termodinamiğin Sıfırıncı Yasası
İki ayrı sistem üçüncü bir sistemde (cisimle) ayrı,ayrı termik dengede ise bu iki sistem termik dengedir.
Şekil 5.9
Sıcaklık ölçüm sonuçlarının gerçekliği bu yasaya dayanır.
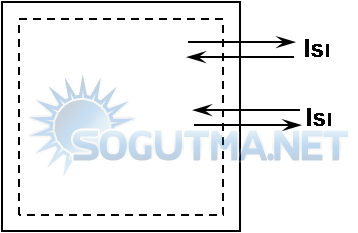
Termodinamiğin Birinci Yasası
Enerjinin var veya yok edilemeyeceğini, ancak bir biçimden diğerine dönüşebileceğini vurgular. Sistemle çevresinin etkileşimi sırasında,sistem tarafından kazanılan enerji çevresi tarafından kaybedilen enerjiye eşit olmak zorundadır.
Şekil 5.10
Enerji, kapaklı bir sistemin sınırlarından iş veya ısı olarak geçebilir.
Birinci yasanın özü toplam enerji adı verilen özelliğin ortaya konmasıdır.
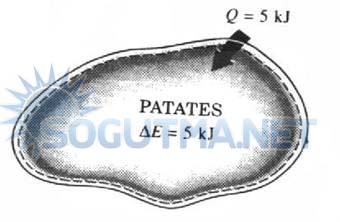
Şekil 5.11
Fırındaki patatesin enerjisindeki artış, patatese geçen enerjiye eşittir.
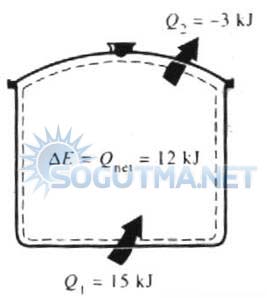
Şekil 5.12
Isı etkileşiminin olmaması durumunda sistemin enerji değişimi net ısı geçişine eşittir.
Şekil 5.12’de ocaktan suya 15 kj ısı geçişi olur ve bunun 3kj kadarı sudan çevre havaya geçerse, suyun enerjisi artarsa 12 kj olur. Buda net ısı geçişine eşittir.
Q=Qnet=∆E
Yukarıda varılan sonuçlar şöyle özetlenebilir; Sistemle çevresi arasında iş etkileşimlerinin olmadığı durumlarda, kapalı sistemin bir hal değişimi sırasındaki toplam enerji değişimi, sistemle çevresi arasındaki net ısı geçişine eşittir.
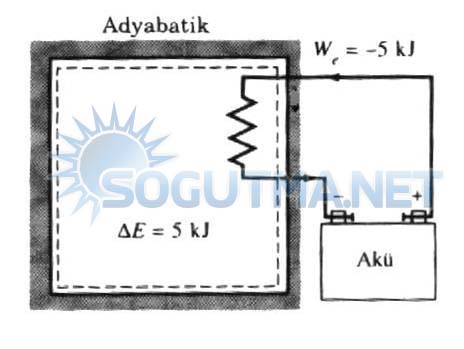
Şekil 5.13
Adyabatik bir sistem üzerinde yapılan iş (elektrik işi), sistemin enerji artışına eşittir.
Yukarıdaki bağıntıda eksi işaretinin yer alması, sistem üzerinde yapılan işin eksi kabul edilmesinden kaynaklanmaktadır. Böylece sistem üzerinde yapılan işin sistemin enerjisini artırması, sistem tarafından yapılan işin de enerjisini matematiksel olarak sağlamış olur.
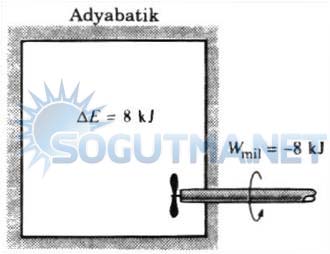
Şekil 5.14
Bir hal değişimi sırasında sistemin enerji değişimi, net iş çevreyle ısı alışverişinin toplamına eşittir.
Yukarıdaki örneklerden, kapalı bir sistemde adyabatik hal değişimi sırasında yapılan iş, sistemin toplam enerji değişimine eşittir.
Eğer bir hal değişimi sırasında hem iş hem de ısı etkileşimi oluyorsa, sonuç her birinin katkısı toplanarak elde edilecektir. Şekil 5.15’de sistemin hal değişimi sırasında sisteme 15kj ısı geçişi oluyor, ayrıca sistem üzerinde pervane tarafından 6kj iş yapılıyorsa, sistemin bu hal değişimi sırasındaki net enerji artışı 18kj olacaktır.
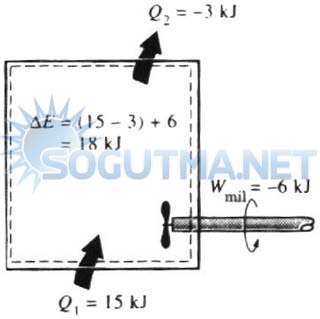
Şekil 5.15
Bir hal değişimi sırasında sistemin enerji değişimi, net iş ve çevreyle ısı alış verişlerinin toplamına eşittir.
Sonuçları genelleştirirsek, kapalı sistem olarak tanımlanan, belirli sınırlar içinde bulunan sabit bir kütle için termodinamiğin birinci yasası veya enerjinin korunumu ilkesi aşağıdaki gibi ifade edilebilir.
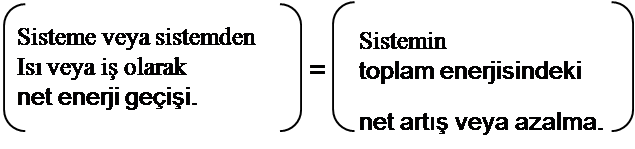
Q-W=∆E (KJ) (5.1)
Q, sistem sınırlarından net ısı geçişini (=∑Qg─∑Qç)
W, değişik biçimleri kapsayan net işi (=∑Wg−∑Wç)
∆E, Sistemdeki toplam enerji değişimi (E2−E1)
Sistemin toplam enerjisi: İç enerji u, kinetik enerji KE ve potansiyel enerji PE. Bu nedenle bir hal değişimi sırasında sistemin toplam enerjisinin değişimi, iç enerji, kinetik enerji ve potansiyel enerjisindeki değişimlerin toplamı olarak ifade edilebilir.
∆E=∆U+∆KE+∆PE (KJ) (5.2)
Bu bağıntıyı 5.1 numaralı denklemde yerine koyarsak
Q−W=∆U+∆KE+∆PE (kj)
∆u=m(U2−U1) (5.3)
∆KE=(m/2) (v22−v12)
∆PE=mg (Z2−Z1)
Örnek Problem 5.1
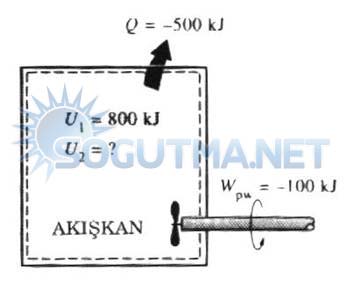
Sabit hacimli kapalı bir kapta bulunan sıcak bir sıvı soğutulurken, bir taraftan’da karıştırılmaktadır. Şekil 17 Başlangıçta sıvının toplam iç enerjisi 800kj’dür. Soğutma işlemi sırasında çevreye 500kj ısı geçişi olmaktadır. Sıvının son haldeki toplam iç enerjisini hesaplayınız
Şekil 5.17
Örmek problem 5-1 genel çizimi
Çözüm
Sistem olarak kabın içindeki sıvı seçilsin. Sistem, sınırlarında kütle geçişi olmadığı için, kapalı sistemdir. Sistem ayrıca hareketsizdir, bu nedenle potansiyel ve kinetik enerji değişimleri sıfırdır.
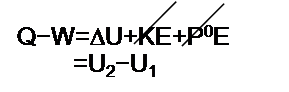
-500kj-(-100)kj=U2-800kj
U2=400KJ
Uygulamada karşılaşılan sistemlerin çoğu hareketsizdir, bu nedenle hızlarında veya kütle merkezlerinin bulunduğu noktada hal değişimi ve sırasında bir değişiklik olmaz. Hareketsiz kapalı sistemlerin kinetik ve potansiyel enerjilerindeki değişmeler gözardı edilebilir. (∆KE=∆PE=0) ve birinci yasayı sadeleştirerek
Q−W=∆ U (kj) (5.4)
Bazı durumlarda iş teriminin Wdiğer ve Ws olarak iki kısımda ele almak kolaylık sağlar. Burada Wdiğer, sınır işi dışında yapılan tüm işlerin toplamıdır. Bu durumda birinci yasa şu şekilde yazılabilir.
Q−Wdğer−Ws=∆E (5.5)
Sistemde olan ısı geçişiyle sistem tarafından yapılan iş artı, sistemden olan ısı geçişiyle sistem üzerinde yapılan iş eksi alınmalıdır.
Örnek 5.2
Bir piston silindir düzeneğinde başlangıçta 300kPa basınçta 25gr doymuş su buharı bulunmaktadır. Daha sonra silindir içindeki bir elektrik ısıtıcısı çalışmakta ve 5dak süresince ısıtıcıdan, 120V kaynaktan sağlanan 0,2A’lik bir akım geçmektedir. Bu süre içinde çevreye 3.7 kj ısı geçişi olmaktadır.
a) Kapalı bir sistemde sabit basınçta gerçekleşen bir hal değişimi için sınır işi Ws ve iç enerji değişimi ∆U’nun birleştirilip entalpi, değişimi ∆H olarak bir terime indirgenebileceğini gösteriniz?
b) Sistemin son sıcaklığını hesaplayınız?
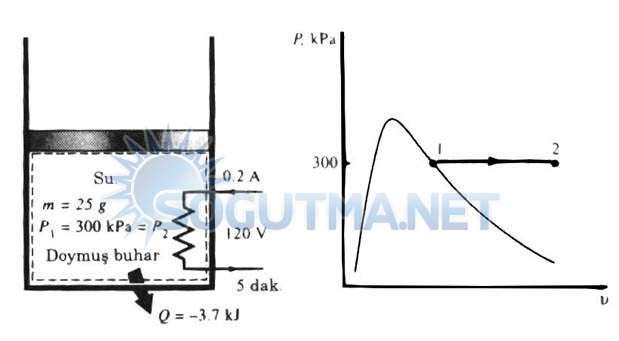
Şekil 5.18
Örnek problem 5.2’nin genel çizimi P-v diyagramı

Hal değişimi, pistonun kütlesi ve atmosfer basıncı sabit kaldığı için basınçta gerçekleşmektedir. Bu durumda sınır işi Ws=P0(V2−V1) = U2−U1 elde edilir.
Fakat P0=P2=P1 Q− Wdiğer=( U2+ P2V2)− ( U1+ P1V1) ayrıca H=U+PV olduğu için
Q− Wdiğer=H2-H1 (kj)
We= V.I.∆t=120V.(0,2A) (300)
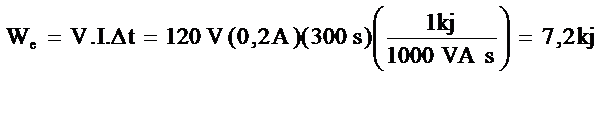
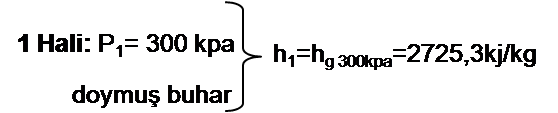
Q−We= m(h2−h1)
−3,7kj−(−7,2kj)=0,025 (h2−2725,3kj/kg)
h2=2865,3kj/kg
Basınç ve entalpi bilindiği için son sıcaklık belirlenebilir.
2 Hali:
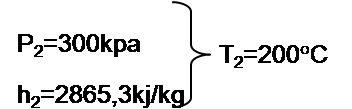
İç Enerji
İç enerji moleküler yapıya ve moleküllerin hareketlilik düzeyine bağlı olup, moleküllerin kinetik ve potansiyel enerjilerinin toplamı olarak düşünülebilir.
Bir sistemdeki moleküller genelde rastgele bir hareket içinde, belirli bir hızla hareket eder, toplu olarak titreşir ve kendi eksenleri etrafında dönerler. Bu hareketin sonucu olarak, bir molekülün yer değiştirme, titreşim ve dönme enerjilerinin toplamından oluşan bir kinetik enerjisi vardır. Sistemin iç enerjisinin, moleküllerin kinetik enerjisiyle ilişkili olan bölümüne duyulur enerji adı verilir.
İç enerji aynı zamanda sistemin molekülleri arasındaki kuvvetlerle ilişkilidir. Bu kuvvetler molekülleri birbirine bağlayan kuvvetlerdir ve tahmin edileceği gibi katı cisimlerde çok güçlü, gazlarda ise daha zayıftır. Katı veya sıvı bir cismin moleküllerine yeterince enerji verilirse, moleküller, aralarındaki kuvvetleri yenip bağları kopararak sistemi gaza dönüştürebilirler. Bu bir faz değişimidir. Eklenen bu enerjiden dolayı gaz fazındaki sistem, katı veya sıvı fazlarına oranla daha yüksek bir iç enerjiye sahip olur. Sistemin fazıyla ilgili bu iç enerjisine gizli enerji adı verilir.
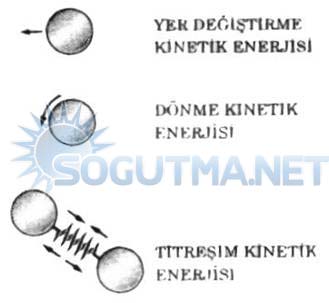
Şekil 5.17
Duyulur iç enerjiyi oluşturan moleküler enerji biçimleri
Yukarıda sözü edilen değişimler, sistemin kimyasal bileşiminde bir değişiklik olmadan gerçekleşebilir. Bir molekülün atomları arasındaki kuvvetlerle ilgili iç enerjiye kimyasal enerji veya bağ enerjisi denir. Yanma işleminde olduğu gibi bir reaksiyon sırasında, bazı kimyasal bağlar bozulurken bazı yeni bağlar oluşur. Bu nedenle İç enerji değişir.
Atom çekirdeği içindeki parçacıklar arasında var olan bağlarla ilişkisi çok büyük miktarlardaki İç enerjiden söz etmek gerekir. (Şekil 5.4.1) Bu enerji, nükleer enerji diye adlandırılır ve nükleer reaksiyonlar sırasında açığa çıkar.
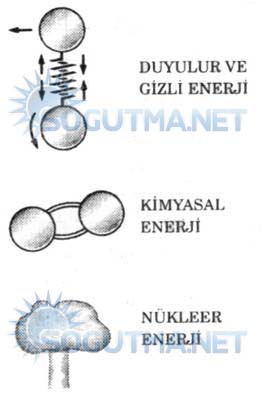
Şekil 5.18
Sistemin İç enerjisi enerji biçimlerinin toplamıdır.
Sistemin toplam enerjisini oluşturan ve yukarıda açıklanan enerji biçimleri, sistem içinde bulunduğu veya depolandığı için enerjinin statik biçimi diye tanımlanabilir. Sistem içinde depolanmayan enerji ise enerjinin dinamik biçimi diye adlandırılabilir. Enerjinin . dinamik biçimleri sistem sınırlarını geçerken algılanır ve hal değişimi sırasında sistem tarafından kazanılan veya kaybedilen enerjiyi gösterir.
Isı Tutumu (Entalpi)
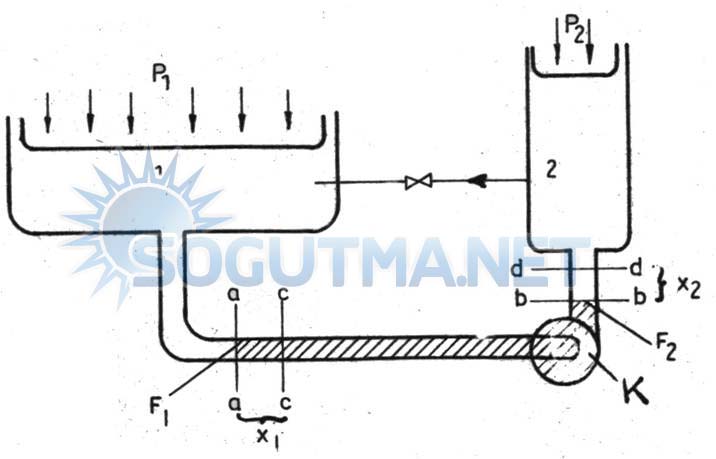
Şekil 5.19
Isı tutumu bir deney düzeneğiyle gösterilmesi
Şekil 5.19‘deki K kompresörü tarafından 1 nolu tanktan gelen soğutucu akışkan buharı emilir. K Kompresörü bu soğutucu akışkan buharını 2 nolu tanka basar. 1 nolu tankta basınç P1, 2 nolu tankta ise P2’dir. Kompresör belirli bir zamanda iş görüp soğutucu akışkanın yerini değiştirerek iş yapmış olur. Belirli bir zaman içinde kompresörün emme ve basma işlemi neticesinde a-a kesiti c-c kesiti yerini, b-b kesitide d-d kesiti yerini alacaktır.
a-a ve b-b kesitleri arasındaki 1 nolu tanktan hareket eden buhar hacminin c-c ve d-d kesitleri arasındaki duruma gelebilmesi için belirli bir iş yapması gerekir. B u iş soğutucu akışkan buharı hacmince absorbe edilen bir iş olup, kuvvetle yolun çarpımına eşittir.
P1.F1.X1 (5.4.2.1)
Burada;
P1:a-a kesitimdeki buhar basıncı
F1:a-a kesitinin alanı
X1:c-c ve a-a kesitleri arasındaki mesafedir.
F1.X1=V1 süpürme hacmi olarak tarif edilmekte olup, bu tarife dayanarak P1 V1 ifadesi süpürme işi olarak isimlendirilir.
a-a kesitindeki buharın iç enerjisi U1 ise c-c kesitinde bu iç enerji P1 .V1 kadar artmış ve ;
U1+P1.V1 olmuştur. (5.4.2.2)
Kompresörde aynı buhara bir L sıkıştırma işi ilave olunur ve kompresörden hemen sonra buharın toplam enerjisi
U1+P1.V1+L (5.4.2.3)
Ancak enerjisi artan soğutucu akışkan buharı basıncı P2 olan 2 nolu tanka basılmak mecburiyetinde olup, basma sırasında toplam enerjisinde:
P2.F2.X2= P2.V2 (5.4.2.4)
Kadar azalma olur, Matematiksel olarak ifade edersek
U1+P1.V1+L− P2.V2=U2 (5.4.2.5)
Bu ifadeyi tekrar düzenlersek
(U1+P1.V1)+L=(U2+P2.V2) (5.4.2.6)
(U1+P1.V1)+L ve (U2+P2.V2) değerleri değişik iki durumdaki buharın ısı tutumunu gösterir.
H=U+P.V kj Toplam entalpi (5.4.2.7)
h=U+P:V kj/kg Özgül entalpi (birim kütle için) (5.4.2.8)
Entropi
Termodinamiğin birinci yasası ısı geçişiyle iş arasında, enerji olarak ayırım yapmaz. Birinci yasa açısından ısı geçişi ve iş eşdeğerdedir. Isı geçişiyle iş arasındaki ayrım ikinci yasa tarafından ortaya çıkarılmaktadır. Başka bir deyişle, entropi geçişinin olmadığı enerji etkileşimi ise iştir. Bir sistemle çevresi arasında olan iş etkileşimi sırasında entropi alış verişi yoktur. Böylece, sistemle çevresi arasındaki iş etkileşimi sırasında sadece enerji alış verişi olur, oysa ısı geçişi sırasında hem enerji hem entropi geçişi söz konusudur. (Şekil 5.20)

Şekil 5.20
Sistem sınırlarından iş geçişi sırasında entropi geçişi olmaz. Ancak, sistem içinde enerji daha az kullanılabilir biçimlere dönüşürken entropi üretimi olur.
Entropi kavramını daha iyi anlayabilmek için özel bir kap içinde sıvı halde bir miktar soğutucu akışkan ele alalım. Bu soğutucun akışkan ∆Q kadar bir ısının tesiri altında kaynamaya terk edildiğinde ve belirli bir sıcaklıkta kaynamaya başladığını düşünelim. Bu durumda entropi diyagramda görüleceği gibi entropilerin farkı (S2−S1) kadar değişmiştir.
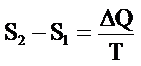 (5.4.3.1)
(5.4.3.1)
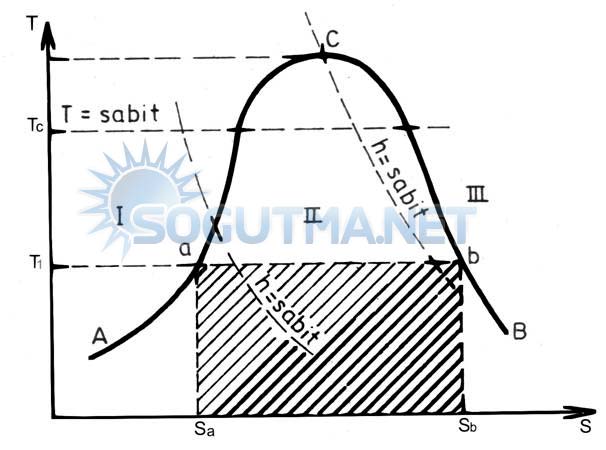
Diyagram 5.5
Sıcaklık entropi diyagramı.
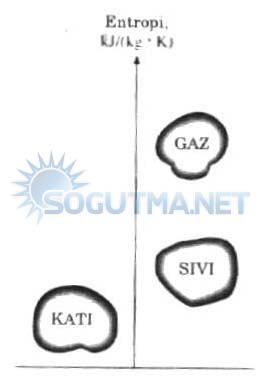
Diyagramı şekil 5.5’te verilen 1No’lu bölge sıvı, 2No’lu bölge sıvı+buhar (yaş buhar), 3No’lu bölge kızgın buhar bölgesidir. A−C eğrisi, sıvı bölgesi ile yaş buhar bölgesini ayıran bir sınır eğrisi olup, alt sınır eğrisi olarak adlandırılır. C−B eğrisi ise yaş buhar bölgesi ile kızgın buhar bölgesini ayran bir sınır eğrisi olup, üst sınır eğrisi olarak adlandırılır. C noktası kritik noktayı göstermektedir.
Herhangi bir soğutucu akışkanı T1 sıcaklığında kaynadığını düşünelim. Diyagram 5.5’te a noktası soğutucu akışkanın sıvı olduğu nokta, b noktası ise soğutucu akışkanın doymuş buhar halinde olduğu noktadır. Böyle bir buharlaşma için gerekli ısı miktarı
q=T1(S2-S1) (5.4.3.2)
olarak hesaplanır. Bu ısı miktarı T-S diyagramında bir alan olarak görülür.
Örnek Problem 5.3
Şekil 5.20’de gösterilen sürtünmesiz piston silindir düzeneğinde başlangıçta 100°C sıcaklığında doymuş sıvı-buhar karışımı su bulunmaktadır. Daha sonra 25°C sıcaklıktaki çevre havaya sabit basınçta bir hal değişimiyle,600kJ ısı geçişi olmaktadır. Hal değişimi sırasında silindir içinde bulunan su buharının bir bölümü yoğuşmaktadır.
a) Suyun entropi değişimini hesaplayınız?
b) Hal değişimi sırasında çevre havanın entropi değişimini bulunuz?
Çözüm
a) Basınç sabit kaldığı için, sıcaklığıda 100°C değerinde kalacaktır.
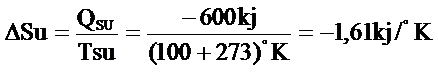
Dikkat edilirse suyun sıcaklığında bir değişiklik olmayıp çevreye verilen ısı, su buharının bir bölümünün daha yoğuşmasına harcanarak entropisinin azalmasına neden olmuştur.
b) Düşük sıcaklıkta ısıl enerji deposu çevre havanın entropi değişimide benzer biçimde hesaplanır. Fakat bu kez ısı geçişi artı değerdedir .Çünkü sistem tarafından verilen ısı çevre hava tarafından alınmaktadır.
QÇevre=-QSİistem=600 kJ
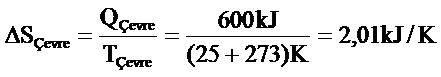
Entropi moleküler düzensizlik veya moleküler rastgelelik olarak görülebilir. Bir sistem daha düzensiz bir hal aldıkça moleküllerin konumları belirsizleşecek ve entropi artacaktır.
Şekil 5.21
Termodinamik dersinin ders notu burada bitmemektedir. 2. Kısmı için Tıklayınız.