Isı Transferi

Isı Transferi bir çok mühendislik dalında bulunan temel bilim dallarından biridir. Isı transferi sayesinde bir çok alanda çok büyük gelişmeler yaşanmış ve yaşanmaya devam etmektedir. Isıtma ve soğutmanın temeli olan ısı transferi temel olarak ısı alış – verişini inceler.
Mühendislik öğrencilerinin özellikle Makine Mühendisliği öğrencilerinin en zorlandığın derslerin başında gelen Isı Transferi konusunu ele aldık ve detaylı bir şekilde sizlere aktarmaya çalışacağız.
ISI TRANSFERİ
Isı bir enerji çeşidi olup yüksek sıcaklıktaki ısıl enerji deposundan düşük sıcaklıktaki ısıl enerji deposuna kendiliğinden geçer. Isı geçişinin olabilmesi için sistemle çevresi arasında mutlaka bir sıcaklık farkı olması gerekir aksi taktirde ısı geçişinden söz edilemez.
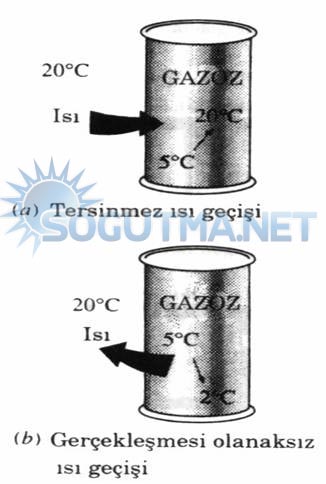
Şekil 8.1
Şekil-8-1’de gösterilen 50C sıcaklıkta bir meyve suyu kutusunu inceleyelim. Meyve suyu kutusunun bulunduğu ortamdan ( yüksek ısıl enerji deposu ) meyve suyuna ısı geçişi olacak belirli bir süre sonra meyve suyunun sıcaklığı yükselecek veya termik dengeye ulaşacaktır. Bu işlemin tersini uygulayacak olursak yani meyve suyunun sıcaklığını başlangıçtaki haline getirmek istersek bu işlem kendiliğinden gerçekleşemez çünkü düşük sıcaklıktaki ısıl enerji deposundan yüksek sıcaklıktaki ısı enerji deposuna kendiliğinden ısı geçişi sağlanamaz.
Düşük sıcaklıktaki ısıl enerji deposundan yüksek sıcaklıktaki ısıl enerji deposuna ısı transfer edebilmek için sisteme dışarıdan bir iş verilmesiyle ( soğutma makinasıyla ) mümkün olmaktadır.
Isı farklı sıcaklıktaki iki ortamdan birinden diğerine geçerken iki ortamın arasında kalan ortamın bileşenlerinide geçmesi söz konusudur. Örneğin dış hava sıcaklığı 40oC olan bir yaz gününde yüksek ısıl enerji deposu dış havadan düşük ısıl enerji deposu odaya geçen ısının duvarın dış sıvasını, tuğla kısmını, iç sıvasınıda geçmesi gibi ;Transfer edilen ısının büyüklüğü sıcaklık farkı yanında yüzeye,zamana ve ortamların fiziksel özelliklerine bağlıdır.
Isı geçişi üç farklı biçimde gerçekleşebilir.
Isı iletimi ( Kondüksüyon )
İletim bir maddenin enerjisi daha fazla olan moleküllerinden yakındaki diğer moleküllere, moleküller arasındaki etkileşim sonucunda enerji geçidir. iletim katı, sıvı ve gaz ortamlarda gerçekleşebilir. Katılarda iletim ısı enerjisinin bir molekülden diğerine aktarılması ile, sıvılarda ve gazlarda ise iletim, moleküllerin rastgele hareketleri sırasında birbiriyle çarpışması sonucunda oluşur. Sıcak bir odadaki soğuk kola kutusu oda sıcaklığına gelirken havadan kolaya alüminyum cidardan iletimle ısı geçişi olur. Şekil 8.2
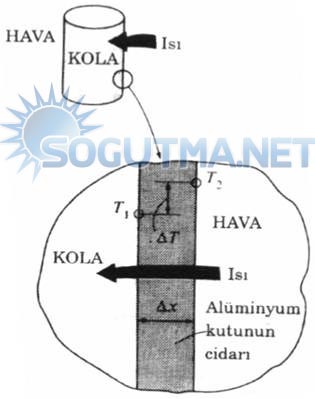
Şekil 8.2
Sıcak havadan soğuk kolaya alüminyum kutunun civarından iletimle ısı geçişi.
∆x kalınlığında bir tabakadan birim zamanda iletimle geçen ısı Qiletim1 sıcaklık farklı ∆T ve ısı geçişine dik alan A ile doğru orantılı tabakanın kalınlığıyla ters orantılıdır. Bu, deneylerle gözlenebilen olgudur. Aşağıdaki gibi bağıntı yazılabilir.
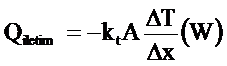
(8.1)
Burada kt ısı iletim katsayısıdır. İletim katsayısı bir maddenin ısı iletme yeteneğinin bir ölçüsüdür.
| Malzemenin Adı |
|
k: kcal/mh0K |
| Kaba sıva (dışta)
Kaba sıva (içte) Buz: 0˚C de -20˚C Cam yünü Mantar levha Pencere camı (ortalama değer)
|
1600
1600 917 920 ― ― ―
|
0,80
0.60 1,90 2,10 0,040 0,036 0,70 |
Çizelge 8.1
Bazı maddelerin ısı iletim katsayıları.
Gümüş, bakır, altın ve alüminyum gibi elektrik akımını iyi ileten maddeler aynı zamanda ısıyı da iyi ilettiklerinden dolayı bu metallerin büyük kt değerleri vardır. Lastik, tahta cam yönü gibi maddeler ısıyı iyi iletemedikler için kt değerleride küçüktür.
İçinde Kaynak Bulunmayan Paralel levhalarda Isı İletimi
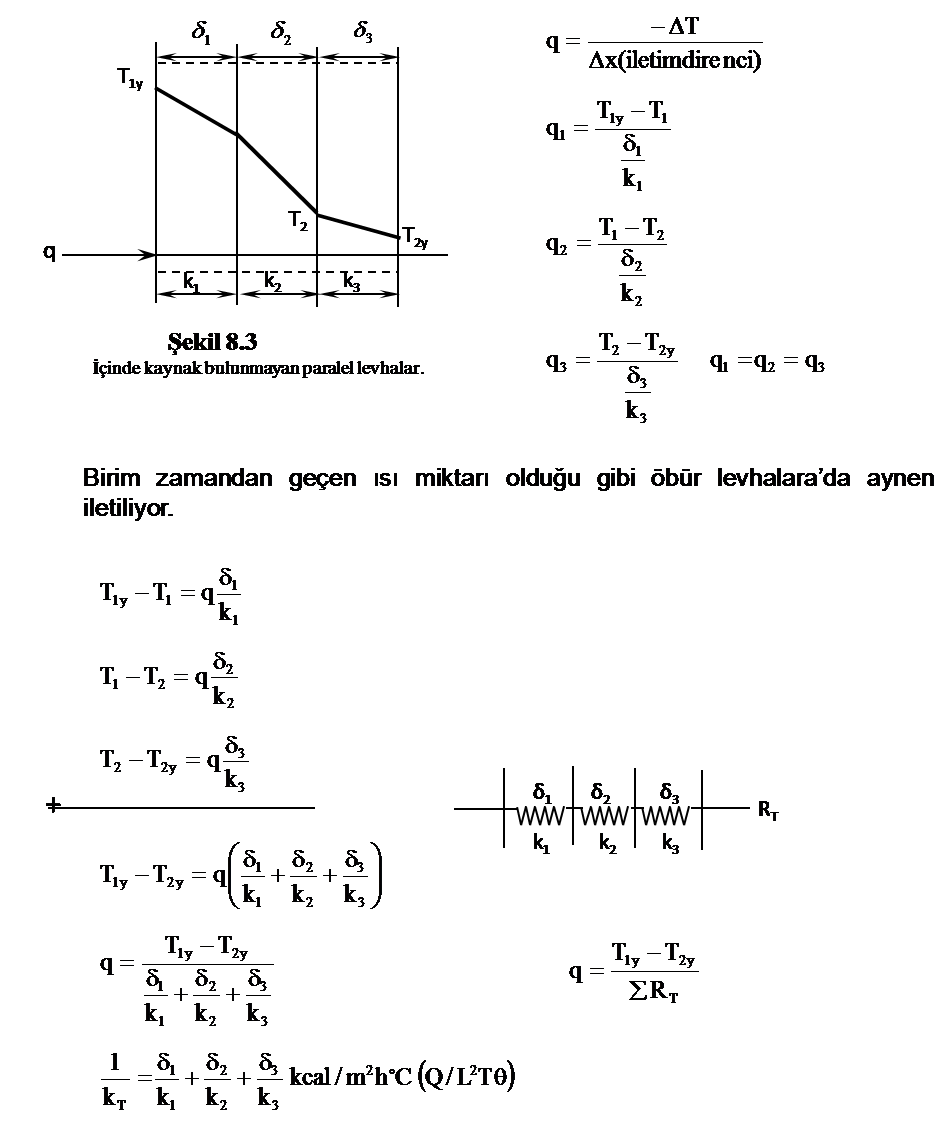
Örnek: Problem 8.1

Isı Taşınımı (Konveksiyon)
Katı bir yüzeyin temas ettiği akışkan bir ortam arasında gerçekleşen ısı geçiş şeklidir.
Paralel Levhaların Her Yanında İki Akışkan Bulunması Hali ve Isı Taşınım Katsayısı ile Toplam Isı Geçiş Katsayısının Belirlenmesi
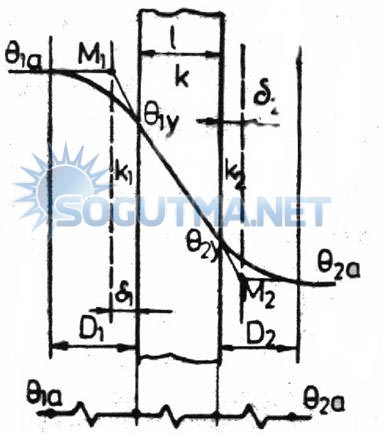
Şekil 8.5
Paralel Levhaların Her Yanında İki Akışkan Bulunması Hali
Üst taraftaki şekilde görüldüğü gibi levhanın her iki yüzeyindeki akışkan sıcaklıkları Q1a>Q2a olmak üzere Q1a ve Q2a olsun. Bu kabule göre Q1a sıcaklığındaki akışkan ile temas eden yüzey sıcaklığı, daha küçük Q1y değerinde, diğer yüzey sıcaklığı ise Q2adan daha büyük Q2y değerinde olup, her iki bölgedeki sıcaklık değişimleri şekilde görüldüğü gibi eğriseldir.
Levha yüzeyleriyle temas eden akışkanların levha yüzey sıcaklıklarına kadar olan sıcaklık değişimleri D1 ve D2 kalınlıklarındaki bölgelerde olur. Düşey eksende sıcaklık değişimleri belirtildiğine göre, Q1y ve Q2y sıcaklıklarının bulundukları seviyelerden bu eğrilere çizilen teğetler Q1a veQ2a sıcaklıklarına uyan yatay doğruların kesişme noktaları olan M1 ve M2 noktalarının yüzeylere olan ve mesafeleri içinde akışkanların hareketsiz oldukları kabul edilebilir. Bu hareketsiz bölge katı cisim gibi düşünülürse ve ısı iletim katsayıları k1, k, k2 ise
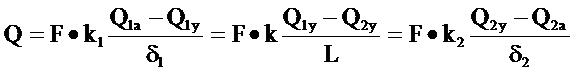
eşitliği yazılabilir. Bu eşitlikteki k/ oranı ısı taşınımı katsayısı olarak adlandırılır ve h ile gösterilir. Bazı literatürde(bilhassa Alman literatüründe) α ile gösterilmektedir. Boyutu Q/L2Tθ olmaktadır. Tarife göre levhanın her iki yüzeyi için Q=F.h1(Q1a-Q1y)=F.h2(Q2a-Q2y) yazılabilir. Geçen ısı miktarı sadece Q1a ve Q2a sıcaklıkları cinsinden, Q=K.F(Q1a-Q2a) ifadesiyle de hesaplanabilir. Burada K, Toplam Isı Geçiş Katsayısı olup Q/L2Tθ boyutundadır ve 1/k=1/h1+1/k1+1/h2 ifadesiyle belirlenir. Dikkat edilirse burada önceki bölümlerden farklı olarak her iki tarafta ısı taşınım katsayısını görmekteyiz. 1/h oranını Isı Taşınım Dirençi olarak adlandırabiliriz. Q ısısı sırayla kalınlığındaki bölgeyi, levhayı ve kalınlığındaki bölgeyi geçtiğine göre
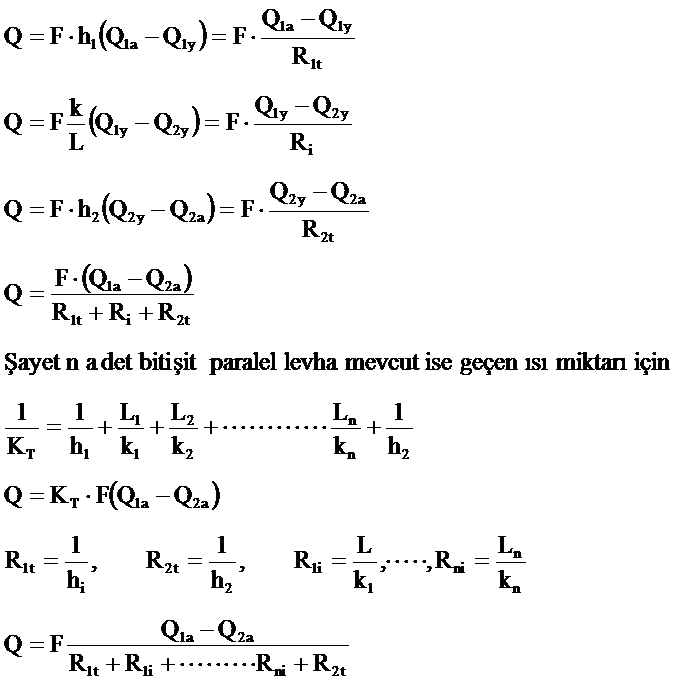
Örnek: Problem 8.2
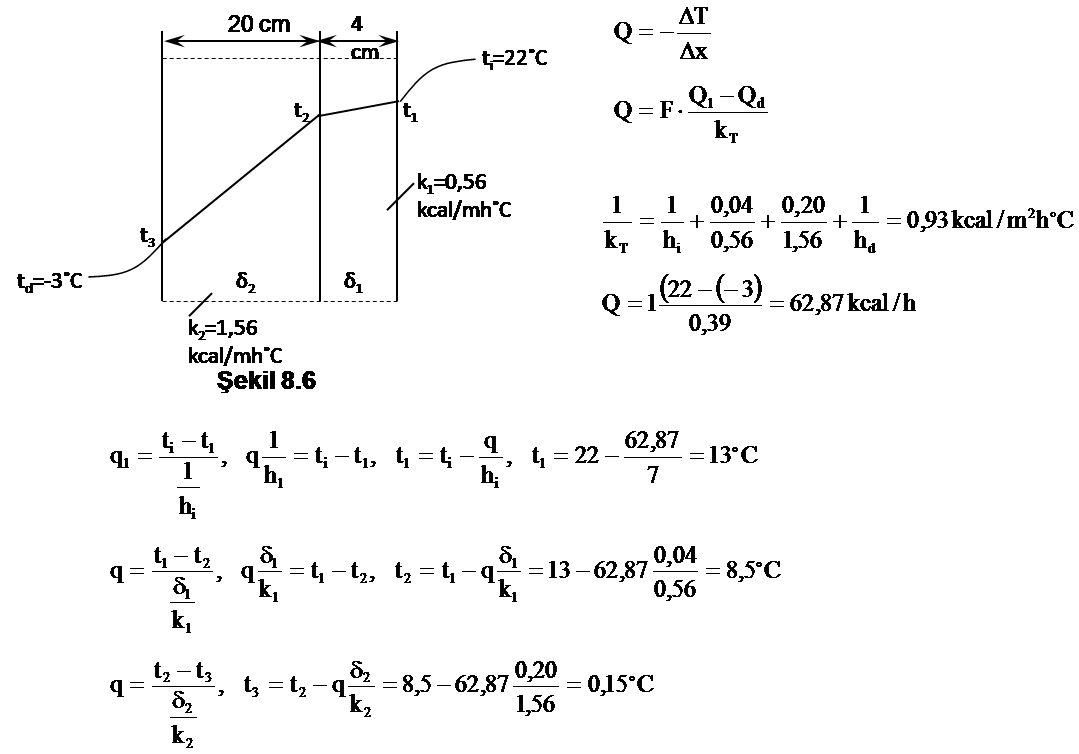
İçice Aynı Merkezli Borularda Isı İletimi
Şekil 8.7
İçice Aynı Merkezli Borularda Isı İletimi
Yukarıdaki şekilde görüldüğü gibi r1, r2, r3 iç yarıçaplarındaki boruların ısı iletim katsayıları k1, k2, k3 ve dış yüzey sıcaklıkları Q1 ve Q2y ara sıcaklıkları Q1 ve Q2 olduğuna göre içice aynı merkezli olan borulardaki ısı iletimi ifadesi için seri dirençlerin toplamı alınarak bulunabilir.
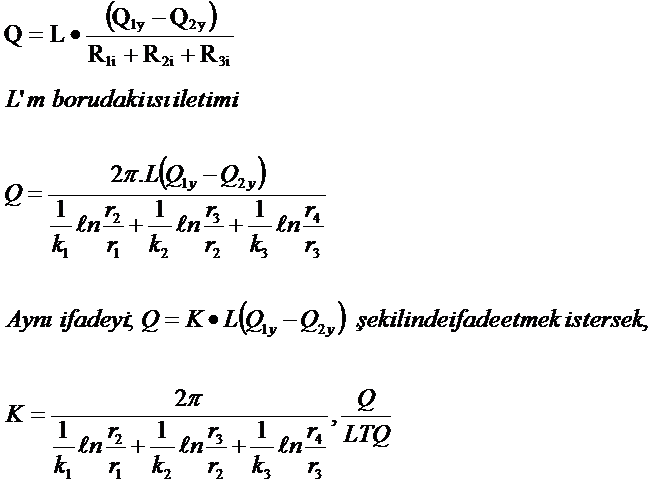
İçice Aynı Merkezli Borularda İçinde ve Dışında Akışkan Bulunması Halinde Isı Taşınımı
Şekil 8.8
İçice aynı merkezli borularda içinde ve dışında akışkan bulunması halinde ısı taşınımı
Şekil 8.2’de görüleceği gibi borunun iç ve dışındaki akışkan sıcaklıkları Q1a ile Q2a, iç ve dış ısı taşımını kat sayıları h1 ve h2 ise aşağıdaki ifadeler yazılabilir.
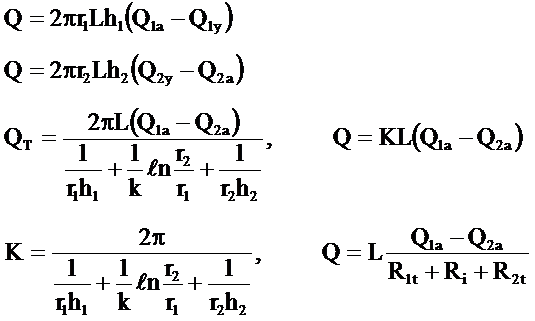
Şayet içice aynı merkezli m adet boru mevcut ise geçen (Q) ısı miktarı akışkan sıcaklıkları 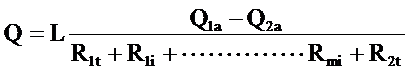 cinsinden.ifadesi yazılır.
cinsinden.ifadesi yazılır.
Örnek Problem 8.3
110×5 mm’lik 20 metre uzunluğundaki bir boru içinden 180˚C sıcaklığında buhar geçiyor. Boru dışındaki sıcaklık 10˚C olduğuna göre 1saatte kaybolan ısı miktarını bulunuz.
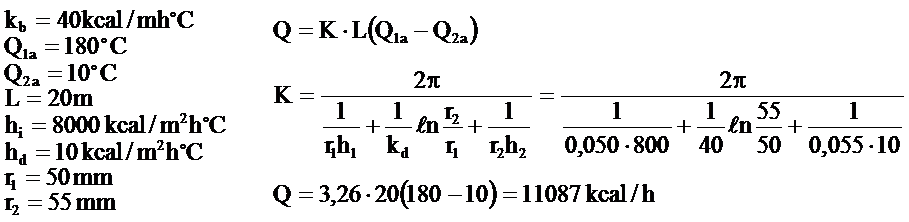
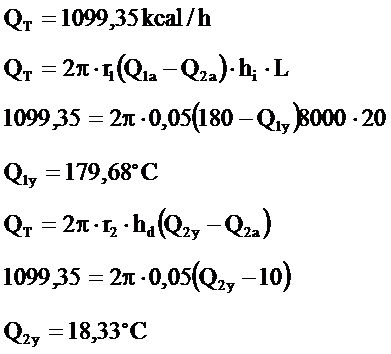
Borularda Sıcaklık Düşmeleri
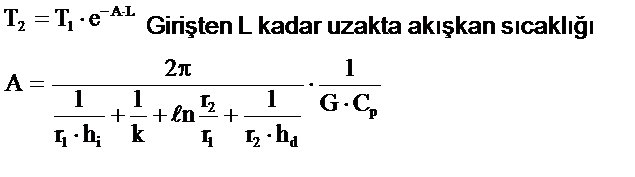
G= Akışkan debisi
Cp=Akışkan özgül ısınma ısısı kcal/kg˚C
Örnek: Problem 8.4
125×4 mm’lik 35m uzunluğundaki bir boru içinden 195˚C sıcaklığında bir akışkan geçiyor. Borunun dışında 49,5mm kalınlığında ve ısı iletim katsayısı 0,05 kcal/mh˚C olan yalıtım malzemesiyle ısı izolasyonu yapılmıştır.
-
İzolasyonsuz boruda 35m sonundaki sıcaklığı bulunuz?
-
İzolasyonlu boruda 35m sonundaki sıcaklığı bulunuz?
a) İzolasyonsuz boruda
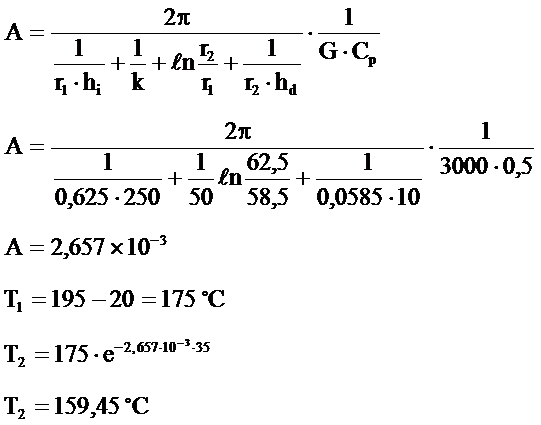
b) İzolasyonlu boruda